一.概念阐述
先上图:
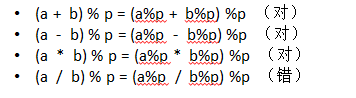
很明显,上述式子只有一条不成立,即 (a/b) % p,但是在有些情况下,又需要进行有模运算的除法。因为式子不成立,如果 a 过大或者 b 过大,极易导致计算过程丢失精度,造成结果误差。因此,为了杜绝这一现象,逆元出现了。
二.逆元定义
**==前提==:模 m 意义下,1个数 a 如果有逆元 x,那么除以 a 相当于乘以 x**
每个数 a 均有唯一的与之对应的乘法逆元 x,使得 a * x ≡ 1(mod p) ,即 (a * x) mod p = 1 mod p, 一个数有逆元的充分必要条件是gcd(a,p)=1,此时逆元唯一存在 。
三.理论铺垫
1.首先根据定义式:
a / x1 = a * x1^-1 //即 a/b = a*b^-1 ,基础乘除转换
inv[x1] ≡ x1^-1 (mod p) //inv[x1] 即为 x1 在模 m 情况下的逆元
a / x1 ≡ a * inv[x1] (mod p) //结论
2.a / x1 ≡ a * inv[x1] (mod p) 等式成立证明:(inv[x1] = x,即 x1 的逆元为 x)
逆元定义:
a * x ≡ 1 (mod p)
a * x mod p = 1,则称 x 为 a 模 p 的乘法逆元。
并且有 (a / x1) mod p = (a * x) mod p //(其中a / x1为整除)
证明:
假设:
a1 / x1 mod p = n (式子一)
(式子一两边同时乘上 x1)
a1 mod p = n * x1 mod p (式子二)
(简化式子二)
a1 ≡ n * x1 (mod p) (式子三)
(式子三两边同时乘上 x, x 为 1 / x1, 即假设 x 为 x1 的逆元)
(根据定义式)
x * x1 ≡ 1 (mod p) (式子四 ,因为 x 是 x1 的逆元,所以得出这个式子)
a1 * x ≡ n * x1 * x (mod p) (式子五)
(式子四带入式子五)
a1 * x ≡ n * 1 (mod p) (式子六)
(式子六化简)
a1 * x ≡ n (mod p) (式子七)
(与式子七变形)
a1 * x mod p = n mod p (式子七)
(式子一带入式子七)
a1 * x mod p = a1 / x1 mod p mod p (式子八)
(等式右边模了一次 p 之后,值肯定比 p 小,因此第二次模 p 无意义,式子八简化)
a1 * x mod p = a1 / x1 mod p (结论) (x 是 x1 的逆元,式子三定义的)
(证毕,有啥问题或者疑问的评论区提出)
四.逆元四大金刚
(瞎取的名字,看起来更加有逼格一点,别问为什么是五个,因为有一个是我,不说了,拯救世界去了。)

1. 费马小定理求逆元
费马小定理:如果p是一个质数,而整数a不是p的倍数,则有a^(p-1)≡ 1(mod p)
很明显,这玩意儿满足求逆元的前提条件,只不过有局限性,那就是 ==p 要为质数==
首先我们翻出我们之前准备好的结论:
a / x1 mod p = a * x mod p (x 是 x1 在模 p 下的逆元) (式子一)
逆元定义:
x1 * x ≡ 1 (mod p) (式子二)
来来来,有眼睛的都发现了,我们把费马小定理的结论带入式子二
x1 * x = x1^(p-1) (式子三) tips:(不懂的爬)
这个式子三很明显了吧,我们现在要求的是逆元 x ,这个化简就不用过多阐述了吧
x = x1^(p-2) (结论)
**由此可得,如果我们想求 x1 的 逆元 x ,那么在 p 为质数的情况下,我们可以用费马小定理求逆元,对于一个数 a 来说,它的逆元 ==inv[a] = a ^ (p-2)==.**
**当然,一般来说,题目给的质素都是超级无敌大,因此,接下来附上一份 ==快速幂==代码供各位太君食用**
#define mod 1e9 + 7
template<typename T> inline T quick_power(T base, T n)
{
T res = 1;
while (n > 0)
{
if (n & 1)
//res *= base;
res = (res * base) % mod;
//base *= base;
base = (base * base) % mod;
n >>= 1;
}
return res;
}
2. 拓展欧几里得求逆元
前置知识:欧几里得算法
- 欧几里得中有一个重要的定理: 对两个不全为0的非负整数不断应用此式:gcd(m,n)=gcd(n,m mod n);直到m mod n为0时。m就是最大公约数
来了来了(拓展欧几里得算法):
毫无疑问,欧几里得算法提供了一种快速计算最大公约数的方法
而扩展欧几里得算法不仅能够求出其最大公约数。而且能够求出m,n和其最大公约数构成的不定方程mx+ny=d的两个整
数x,y(这里x和y不一定为正数)。
在欧几里得算法中,终止状态是n == 0 时,这时候其实就是 gcd(m,0);我们想从这个最终状态反推出刚开始的状
态。由欧几里得算法可知。gcd(m,n) = gcd(n,m mod n);
那么有如下表达式:
gcd(m,n) = m*x1+n*y1;
gcd(n,m mod n) = n*x2+(m - m/n*n)*y2;
(此处的m/n表示整除,例如:6/4 = 1;所以:m mod n = m % n = m - m/n*n)
化简上式有:
n*x2 + m * y2 - m/n*n*y2 = m*y2 + n*(x2 - m/n*y2)
与原式 gcd(m,n) = m*x1+n*y1;对比,容易得出:
x1 = y2; y1 = x2 - m/n*y2;
根据上面的递归式和欧几里得算法的终止条件n == 0,我们可以很容易知道最终状态是m * x1 + 0 * y1 = m
==来来来,太君们吃点餐前小点==:
template<typename T> inline T ex_gcd(T a,T b,T &x,T &y) //拓展欧几里得
{
if(b==0)
{
x=1;
y=0;
return a;
}
T r = ex_gcd(b,a % b,x,y);
T t = x;
x = y;
y = t - a / b * y;
return r;
}
m*x+n*y=gcd(m,n); 这个方程也被称之为“贝祖等式”。它说明了对a,b和它们的最大公约数d之间的线性方程。
一定存在整数x,y使得m*x+n*y=gcd(m,n)成立。
从这里也可以得出一个重要推论:
a,b互质的充要条件是方程 ax+by = 1必有整数解。
现在来讨论一个更一般的方程:ax + by = c(a,b,c都是整数)。
这个方程想要有整数解,那么根据扩展欧几里得算法我们知道,当且仅当 m 是d = gcd(a,b)的倍数时有解 ,同时有
无穷多组整数解。
我们知道了线性方程 ax + by = c 有整数解的条件,并且根据上述算法,也能求出一组方程的解。但是
这组解很可能包含负数。
我们通常的需求是最小的特解。也就是这个不定方程的最小正整数解。
该了解的都了解了,那到底怎么用拓展欧几里得求逆元呢?
**把 a * x = 1( mod p)称为 a 关于 1 mod p 的乘法逆元。 它的解其实就相当于寻找方程 ax+py=1 (不理解的话重新看有整数解的判定条件)的解。根据乘法逆元的性质,==只有当 a 与 p 互素,a 关于模 p 的乘法逆元有解。如果不互素,则无解==。那么这个方程就是 a,b 互质的充要条件是方程 ax+by = 1 必有整数解。**
==等不及了吧,我就知道,快食用正餐吧==:
template<typename T> inline T mod_reverse(T a,T n) //ax=1(mod n) 求a的逆元x
{
T d,x,y;
d=ex_gcd(a,n,x,y);
if(d==1)
return (x%n+n)%n;
else
return -1; //没有的话返回 -1
}
3. 线性递推求逆元
这玩意儿没有弯弯绕,就是推导的过程,略有点抽象(与我而言),直接上图:

看懂了不,没看懂就和我这个蒻鸡一起记板子吧(哭了)
// mod 是 质数
long long inv[maxn];
void getinv(ll mod)
{
inv[1] = 1;
for(int i = 2;i<=mod-1;i++)
inv[i] = (mod-mod/i)*inv[mod%i]%mod;
}
4. 欧拉定理求逆元
欧拉定理:若a、p互素,则有a ^ φ( p) ≡ 1(mod p)(费马小定理的一般形式)
φ(( p ) - 1) ∗ a ≡ 1(mod p)
a ^ (φ( p )−1)就是 a 在mod p意义下的逆元啦。
至于φ( p )怎么推导计算的的,我这个蒻鸡实在理解不了-->> 太君移步
直接上板子:
template<typename T> inline T phi(T x) //欧拉函数
{
T ans = x;
for(int i = 2;i*i<=x;i++)
if(x%i==0)
{
ans = ans/i*(i-1);
while(x%i==0) x/=i;
}
if(x>1)
ans=ans/x*(x-1);
return ans;
}
long long Phi[max_n];
inline void euler(long long N) //欧拉筛法,批量求欧拉函数结果
{
Phi[1] = 1;
for(int i = 2;i<N;i++)
if(!Phi[i])
for(int j = i;j<N;j+=i)
{
if(!Phi[j])
Phi[j] = j;
Phi[j] = Phi[j]/i*(i-1);
}
}
**==够不够?不够再来一个==**
long long tot = 0; //质数个数
long long prime[maxn]; //质数
inline void Euler(long long N) //欧拉筛优化
{
Phi[1] = 1;
for(int i = 2;i<N;i++)
{
if(!Phi[i])
Phi[i] = i-1,prime[tot++] = i;
for(int j = 0;j<tot&&(long long)i*prime[j]<N;j++)
if(i%prime[j])
Phi[i*prime[j]] = Phi[i]*(prime[j]-1);
else
{
Phi[i*prime[j]] = Phi[i]*prime[j];
break;
}
}
}
五.阶乘逆元
顾名思义,就是阶乘的逆元,顺道提一下,可能有助于排列组合的计算,没啥好说的,继续上板子:
//阶乘逆元
#define ll long long
ll fac[1000000+5]; //阶乘
ll inv[1000000+5]; //逆元
void getfac()
{
fac[0] = inv[0] = 1;
for (int i = 1 ; i <= 1000000 ; i++)
{
fac[i] = fac[i-1] * i % mod;
inv[i] = quick_power(fac[i],mod-2);
//表示i的阶乘的逆元
}
}
//组合数
inline ll getC(ll n,ll m)//C(n,m) = n!/((n-m)!*m!) % mod
{
return fac[n] * inv[n-m] % mod * inv[m] % mod;
}
//当 n,m 过大时,可以用Lucas定理降数据
inline ll Lucas(ll n,ll m)
{
if(n < mod && m < mod) return getC(n, m);
return Lucas(n/mod, m/mod) * getC(n%mod, m%mod)%mod;
}
---------------------------------------------------
//排列数
inline ll getA(ll n,ll m) //A(n,m) = n!/(n-m)! % mod
{
return fac[n] * inv[n-m] % mod;
}
六.小结
一般,对于用到逆元的题目,p 一般都为质数,因此个人建议先把费马小定理求逆元先掌握,所以我对费马小定理求逆元的推导做的十分详细,如果遇到 p 不是质数,那么建议直接上欧拉求逆元。最后呢,可以根据实际情况选用线性递推求逆元,或者阶乘逆元。
相关例题,大家可以去 牛客 啊,洛谷 之类的一些OJ上找,直接搜知识点就行,看完要巩固。
有啥问题的,欢迎指出,我好改正。
